The Magic of Synthetic Data

How GANs Can Help You Generate Artificial Data that is Representative of Your Original Data

Synthetic data, or data augmentation, is the process of creating new, artificial data that is similar to the original data. This is typically done using generative adversarial neural networks (GANs), which are composed of two neural networks that compete with each other to generate and identify synthetic data. The first network, the “generator,” attempts to create new data that is similar to the input data, while the second network, the “discriminator,” tries to identify which data is synthetic and which is not. Through this competition, the GAN is able to generate new, synthetic data that is representative of the original data. This can be useful in a variety of applications, such as improving the performance of machine learning algorithms and increasing the size of a dataset for analysis.

Some answers

I have seen that whenever someone talks about the synthetic data (or rather data augmentation), there is always someone who asks how it is possible that a larger dataset can be created from a few rows.

Is it something magic, or are we inventing the data? Well, we could say that both things are somewhat true. It’s magical because generative adversarial neural networks (or GANs) are amazing. And there is some truth in the fact that we are inventing the data because these GANs are fed with random data as input. Let’s take a closer look.

The funny game of GANs

The idea was to build 2 different neural networks and pit them against each other. The starting neural network generates new data that is similar to the input data. The second neural network is tasked with deciding which data is artificially generated and which is not. Both networks are always competing with one another, with the first one attempting to trick the second and the second attempting to figure out what the first is doing. The game finishes when the second network cannot “discriminate’” between data from the first network output and the original data. This is why we call the the first network “generator” and the second network “discriminator”.

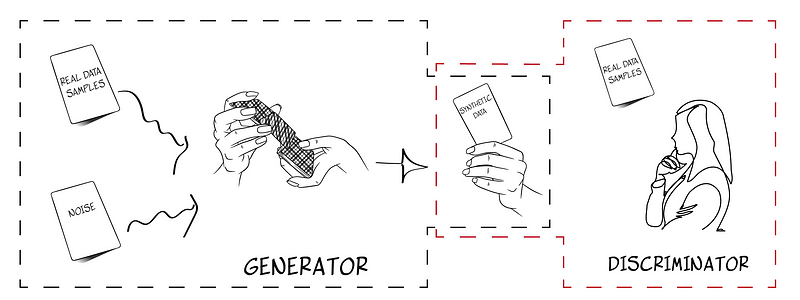
It’s as simple as it seems; however, some properties make it so. Consider a one-dimensional data set. If we draw it, we will get a straight line with a sequence of points distributed along it. We want to create synthetic data out of this original data. It is plausible that we will place points along that line, within the limits set by the original data. To ensure that this new data is representative of the original data (and therefore “equivalent”), we will follow some requirements. For example, we will make the new data have the same mean and standard deviation as the original data, and their probability distribution will be the same too. So if we use a standard statistical hypothesis tests like for example chi-squared test, we will confirm that both data sets comes from the same probability distribution.

Concentration of distances

If, instead of a one-dimensional data set, we have, say, a data table with one hundred columns (so 100-dimensional), we can imagine repeating the same process but on a high-dimensional sphere rather than a line. The steps are the same. But it’s even simpler for the GAN. And this does not necessarily make things more difficult for the GAN.

In high-dimensional spaces we observe a unique phenomenon known as “concentration of distances” . For example, if we compute the distance between all the points in our line of points, we will get a value for the maximum distance and another for the minimum distance. These two numbers are quite close in a high-dimensional space (if the number of dimensions is infinite, these two values are equal). What exactly does this mean? In high-dimensional spaces, points are concentrated in a certain area. That is why the GAN will find it easier to “place” new points within that area. This phenomenon is both the advantage and the critical point for a GAN: advantage because makes thinks easy, and critical point because if GAN cannot detect this area, it will be unable to generate synthetic data (pathology known as “mode collapse”).

Once we have generated new synthetic data, discriminator has to decide whether this data is synthetic or not. If the “discriminator” notices any differences in the data that lead her to believe it is fake (synthetic), she will reject it and request more data from the “generator.” So long as the “discriminator” believes the data isn’t fake.

¿Can this data reveal more insights than original data?

Finally, we can have a dataset with many more samples than the original. This data has been subjected to a first filter, the “discriminator.” But we want to make sure that this data “looks like” the original. So we could repeat this assessment using one of the many techniques developed for this purpose. The question is now ¿Can this data reveal more insights than original data?. The answer is yes. Many algorithms used to get insights from data needs a minimum number of samples. Is this number is particularly low the algorithm will not be able to identify if a certain “pattern” is indeed a “pattern”.