How to build a Digital Twin

In this tutorial, we will show how to create a simple but functional Digital Twin in Python. A Li-ion battery will be our physical asset. This Digital Twin will enable us to analyze and predict battery behavior, and it can be integrated into any virtual asset management workflow.

Virtual systems and digital twins

Digital twins are a critical component of Industry 4.0. Its basic principle is to replicate physical assets in a virtual world in order to model its dynamics. Imagine we have a water pump somewhere in a city’s water pipe network. Water pumps consume energy and release it in the form of water flow and pressure. The term “replica” refers to the creation of a virtual object capable of simulating this behavior.

This pump is part of the overall water pipe network system, along with pipes, valves, meters, and other accessories or sub-systems. These subsystems are all linked. Virtualizing the system entails doing the same for all subsystems. After that, we may simulate the entire system, including its dependencies. A virtual system’s goal is to imitate the physical world in order to introduce alterations, evaluate performance, or predict scenarios in which this asset or subsystem is involved (for example, in maintenance tasks).

A digital twin, as previously defined, is a virtual object that represents a subsystem. This “twin” is expected to respond to input variables in the same way that its “physical twin” does. This virtual object must integrate a model to do this. The most important feature of the digital twin is a model that can simulate “physical” behavior in a digital context. Please keep in mind that when we say “physical,” we mean any real-world entity (can be a Li-ion battery, a water pump, a person, a city or a cat). Anything that can be modeled can be virtualized (figure 1).

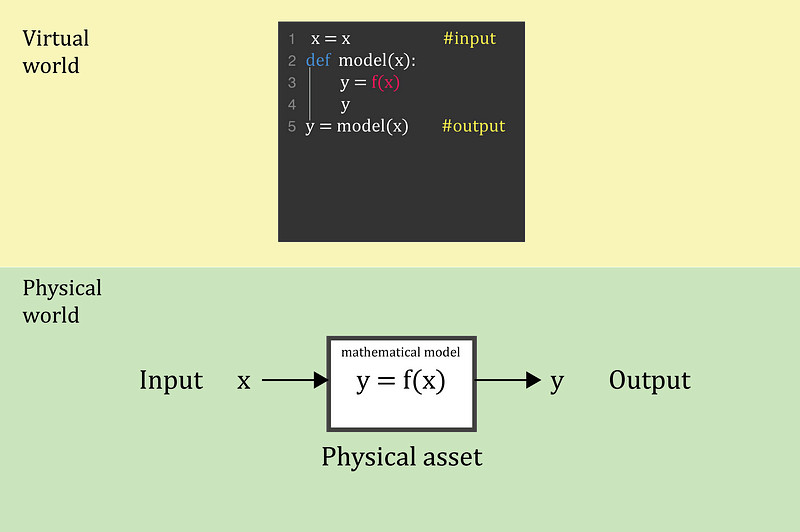
Digital model of Lithium-ion battery

Rechargeable lithium-ion batteries are a cutting-edge battery technology that relies on lithium ions in its electrochemistry. These batteries are important assets for applications such as electric vehicles and energy storage in electric distribution networks, in addition to portable tech devices. The most critical aspect of these batteries is their cost of aging. After repeated charge-discharge cycles, batteries’ cells degrade, resulting in a reduction in charging capacity. This phenomenon has been a key research area in the development of longer-lasting batteries. Its modeling has likewise been a contentious topic. Battery degradation has an important impact the above mentioned technologies planning and operations.

The physics of battery life degradation is quite complicated. Some semi-empirical lithium-ion battery degradation models for measuring battery cell life loss have been proposed in recent years (Chu et al., 2018; Laresgoiti et al., 2015). End-of-life batteries are commonly characterized as those that only offer 80% of their rated maximum capacity. This degradation can be written as follows using one of the empirical models (Chu et al., 2018):

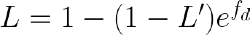
where 𝐿 is the battery life-time, 𝐿′ is the initial battery life-time and 𝑓_d is a linearized degradation rate per unit time and per cycle (Chu et al., 2018). This rate can be written as well as a function of discharge time - 𝑡, the discharge cycle depth -δ, the average cycle state of charge -σ and the cell temperature -𝑇𝑐.

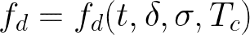
Experimental data

Our model must forecast battery life based on the information we’ve . However, we would like to compare this model to measurements taken in order to determine the accuracy of our model. Let us pause here for a while.

Many digital twins are not based on exact physical models and only use experimental datasets and machine learning algorithms. This is a very cool method of doing things. They can, for example, build a model using a deep neural net to capture the true dynamics of the data. However, generalizing this model to other objects needs working with a large number of samples in order to obtain a reliable general model. On the other hand, when working with physical models, we require less data to obtain an accurate general model.

We will leverage real data from charge-discharge cycles in lithium-ion batteries to build our digital twin. We will use Li-ion Battery Aging Datasets available from NASA Ames Prognostics Center of Excellence (PCoE). This dataset will be valuable in determining the accuracy of our physical model and to improve it. We will use the data associated with battery number 5. We will plot the ‘Capacity’ feature with the number of cycles and compare it to our physical model. Before we begin, we will substitute the variable 𝐿(battery life-time) for C (battery capacity). Equation 1 will be written as follows:

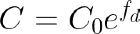
where 𝐶 is the battery capacity and 𝐶_0 is the initial battery capacity. For 𝑓𝑑 we have used the following approximation:

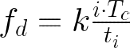
where 𝑖 is the charge-discharge cycle, 𝑇𝑐 the temperature measured in the cell during the cycle, 𝑡𝑖 is the discharging time and 𝑘 and empirical constant with value 0.13 .

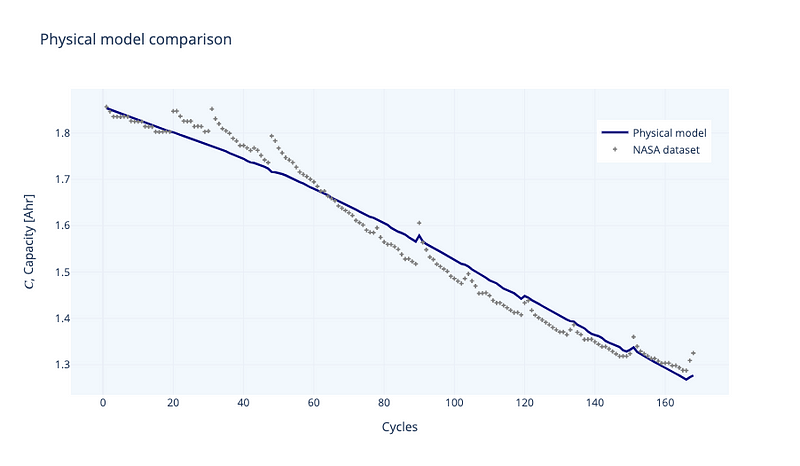
Figure 2 illustrates the results. Our model accurately predicts the observed values (we get a Mean Absolute Error — MAE of 0.004). The model is supposed to gather a battery capacity behavior in which the capacity decreases slowly during the first cycles and then accelerates after a particular point. These changes are subtle, and many engineers utilize simple linear models to approximate this behavior. Our model is semi-empirical and includes various adjustments to avoid dealing with PDEs (partial differential equations).

Building a hybrid digital twin

We could our “model” to directly create a digital twin. But, in order to apply Machine learning, we are going to use it to improve our model using the experimental data from NASA dataset. Our proposal is shown in figure 3.

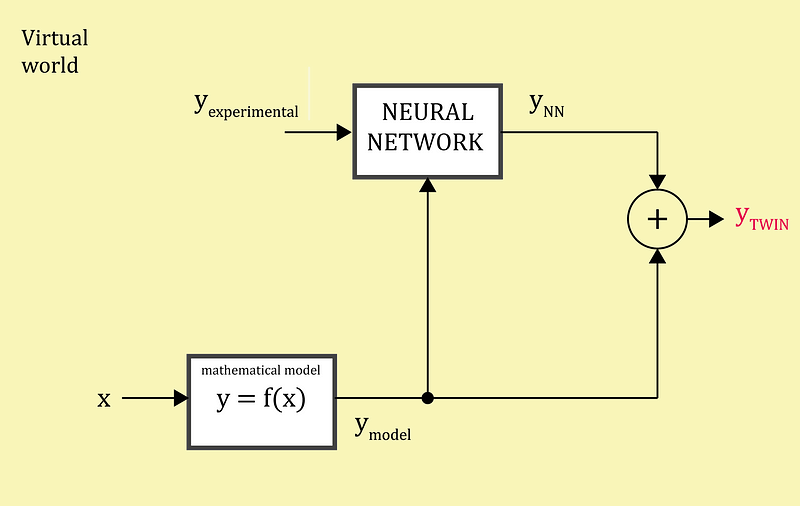
We are improving our mathematical using experimental data and our model’s output using a NN.

##### Define inputs and outputs
###### input: the simulation capacity 
X_in = (dfb['C. Capacity'])
output: difference between experimental values and simulation
X_out = (dfb['Capacity']) - (dfb['C. Capacity'])X_in_train, X_in_test, X_out_train, X_out_test = train_test_split(X_in, X_out, test_size=0.33)

###### We are using a very simple neural network

model = Sequential()
model.add(Dense(64, activation='relu', input_shape=(1,)))
model.add(Dense(32, activation='relu'))
model.add(Dense(1))

###### Compilation
epochs = 100
loss = 'mse'
model.compile(optimizer = SGD(learning_rate=0.001),          
                          loss=loss,
                          metrics=['mae'], #Mean Absolute Error
)
history = model.fit(X_in_train, 
                    X_out_train, 
                    shuffle=True, 
                    epochs=epochs, 
                    batch_size=20, 
                    validation_data=(X_in_test, X_out_test),
                    verbose=1)

The comparison’s result:

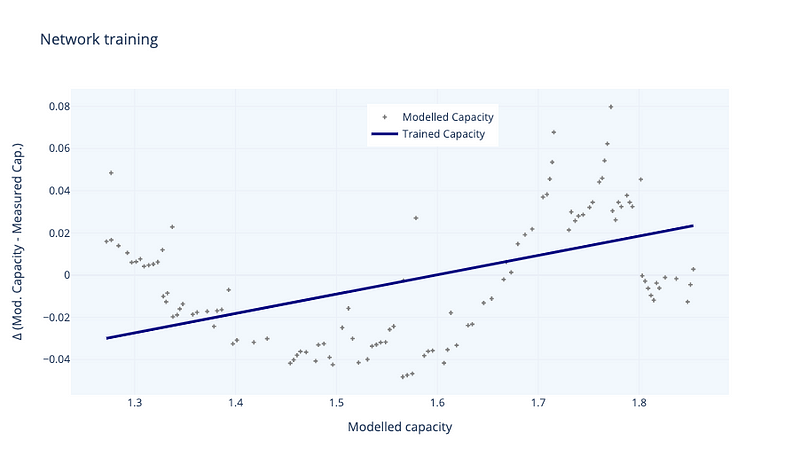
As we can see in figure 4, NN learns a basic understanding of the differences between our mathematical model and the experimental results. Now we can add this learning to our mathematical model to improve it:

# Our digital twin by improving our model with experimental data
X_twin = X_in + model.predict(X_in).reshape(-1)

And that’s it. We have our digital twin (or hybrid twin) in witch:

• We have created a physical model (or mathematical model)
• We have compared our model with experimental data.
• With this comparison, we were able to improve our model.

Finally, we have a “twin” of this battery in our virtual environment that is expected to perform similarly to its real-world counterpart. Next, we’d like to contrast our mathematical model with that of our digital twin:

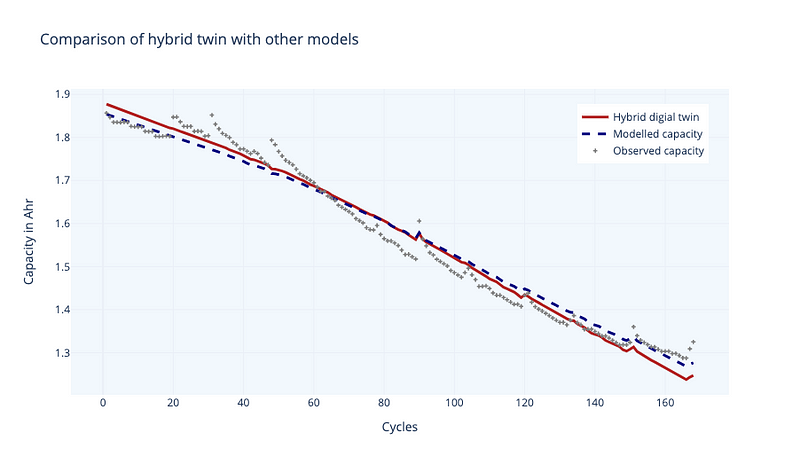
Figure 5 shows how our digital twin has improved our model modestly. The benefit of a hybrid digital twin is that it allows us to employ a semi-empirical mathematical model and refine it using experimental data. It has advantages over both, a particularly mathematical model since it can be improved, and an ML model because it is more general (so could be applied for example to other battery obtaining better accuracy than a ML model alone).

Prediction

With our digital twin we can make predictions in order to operate the Li-ion battery.

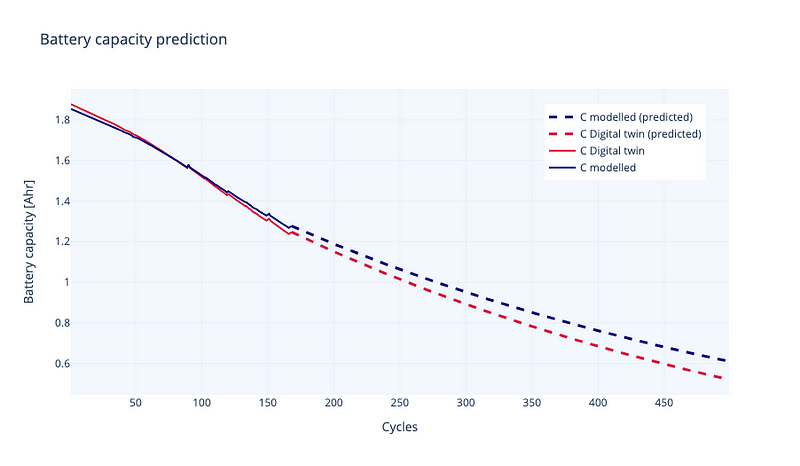
Conclusions

Digital twins are an emerging topic in the field of Industry 4.0. We’ve shown how to use Python to make a minimal digital twin. When we have experimental data sets, we can show how “hybrid” digital twins are a more realistic way to virtualize assets. Furthermore, less data is required to develop reliable models. We can add more future experimental data measurements to our digital twin to improve even more our mathematical model.

Libraries

We have used Keras library for NN and Plotly for plots.

Acknowledgments

To professor Merten Stender from Hamburg University of Technology, m.stender@tuhh.de and its work Digital twin for structural dynamics applications (here).

Code and data

You can find this code in the repo and data here (Li-ion Battery Aging Datasets).

Citations

• B. Xu, A. Oudalov, A. Ulbig, G. Andersson and D. S. Kirschen. (2018). Modeling of Lithium-Ion Battery Degradation for Cell Life Assessment. in IEEE Transactions on Smart Grid, vol. 9, no. 2, pp. 1131–1140. doi: 10.1109/TSG.2016.2578950.
• I. Laresgoiti, S. Käbitz, M. Ecker, and D. U. Sauer. (2015). Modeling mechanical degradation in lithium ion batteries during cycling: Solid electrolyte interphase fracture. Journal of Power Sources, vol. 300, pp. 112–122 .