Physics Meets AI: How Symmetry Could Help Us Understand Language Models

In the world of science, physics has long been our guide to understanding the universe’s fundamental laws. But what if these same…

In the world of science, physics has long been our guide to understanding the universe’s fundamental laws. But what if these same principles could help us unlock the mysteries of artificial intelligence, specifically in Large Language Models (LLMs)? This article explores how concepts from physics, particularly symmetries and transformations, can provide new insights into AI alignment — ensuring AI systems behave in ways that align with human values and intentions.

“It is only slightly overstating the case to say that physics is the study of symmetry.”

Philip Anderson, Nobel Prize winner

Understanding Symmetries

Let’s begin with a basic but deep concept: symmetry. Imagine rotating a perfect circle; it appears the same thereafter, right? That’s symmetry in action, and it’s much more than just a nice visual function. Symmetries in physics are transformations that preserve certain attributes of a system. These symmetries are more than just mathematical curiosities; they are the foundation of our understanding of the universe. Here’s why they are so important:

• Fundamental Laws

Nature’s symmetries give rise to many of physics’ most fundamental laws, such as energy conservation and relativity.

• Unification of Forces

Symmetries have resulted in the convergence of apparently divergent forces. For example, symmetry concepts were used to unify the electromagnetic and weak nuclear forces.

• Particle Predictions

The Standard Model of particle physics, our most complete theory of fundamental particles, was largely built on symmetry principles. It even anticipated the existence of particles such as the Higgs boson before they were empirically discovered.

• Simplification

Symmetries frequently simplify difficult problems, making seemingly unattainable calculations manageable.

• Deep Insights

These symmetries frequently reveal profound truths about how the universe works at its most basic level.
In general, symmetries in physics are more than just observations; they are powerful instruments that have frequently revealed new insights into nature’s innermost mysteries. By extending this strong concept to AI and language models, we hope to get similar profound insights into how these complex systems function.

Symmetries in Language Models

Now, let’s apply this idea to language models. In LLMs, words are represented as points in a high-dimensional space called an embedding space. Each word is like a star in this vast galaxy of meaning. Just as we can rotate objects in our 3D world, we can perform transformations in this embedding space. These transformations might reveal hidden patterns in how language models understand and process information.

To illustrate this, we have made a simple experiment using BERT, a popular language model. We know BERT embedding space has 768 dimensions. However, we will only analyze three dimensions to visualize the results using PCA. We “rotated” the embedding of the word “happy” towards “ecstatic”. Here’s what we found:

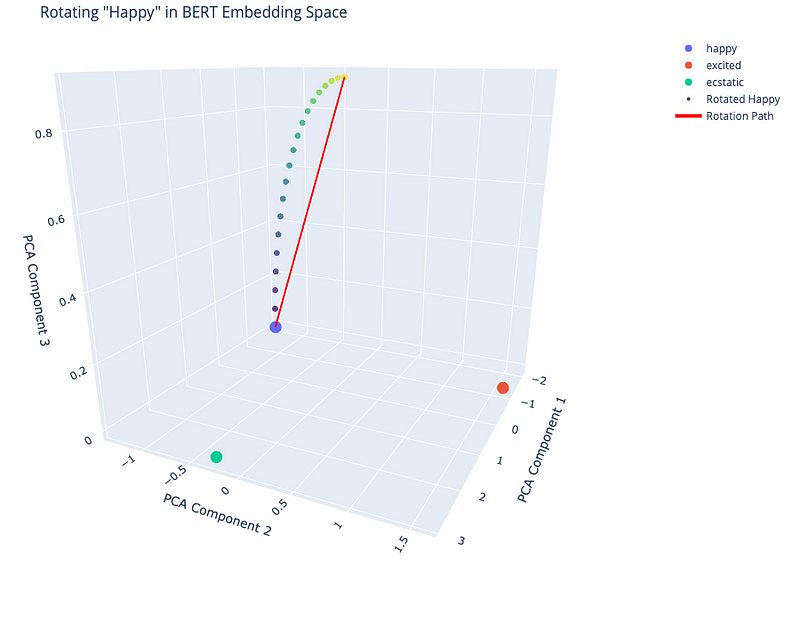
1. The rotation created a smooth path from “happy” to “ecstatic”.
2. Interestingly, the word “excited” wasn’t directly on this path, suggesting complex relationships between words in the embedding space.

This experiment shows how we can use mathematical transformations to explore the semantic space of a language model. It’s like having a map of the AI’s understanding of word-to-concept relationships. And this map has certain distinctive features that will allow us to infer analogous transformations in critical domains, such as model bias and model reasoning.

Noether’s Theorem and Conservation Laws

In physics, there’s a profound connection between symmetries and conservation laws, thanks to Noether’s Theorem. For every symmetry in a physical system, there’s a corresponding quantity that’s conserved. For example, if we perform an experiment today or tomorrow (time translation), the laws of physics remain the same. If the laws of physics remain constant at all times, the system’s behavior does not depend on absolute time. This independence from absolute time implies the existence of a constant quantity (energy) while the system evolves. We deal with energy conservation.

Could there be similar “conservation laws” in language models?
If we find symmetries in how a model processes language, these might point to fundamental rules governing the model’s behavior. This could be a powerful tool for understanding and aligning AI systems. For instance, if we identify transformations that consistently preserve certain properties (like sentiment or factual accuracy) across different contexts, we might have found a “conservation law” of the language model. This could help us predict and control the model’s outputs more reliably.

General Covariance in embedding spaces

In physics, general covariance principle states that the contents of physical theories should be independent of the choice of coordinates needed to make explicit calculations. Einstein’s theory of general relativity is based on two very subtle principles: a physical principle known as the equivalence principle and the general covariance principle. Gravity, in general relativity, is viewed as the curvature of spacetime rather than a force. This description is covariant since it does not rely on a certain coordinate system. The curvature of spacetime influences the velocity of objects in a predictable way for all observers, independent of frame of reference.

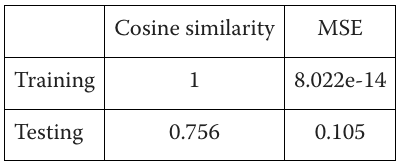
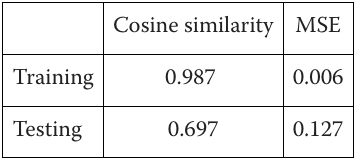
In language models, we can think of this as the idea that the meaning of a word should transform predictably when the context changes (equivalent to coordinates changing). We tested this idea using BERT by changing the tense in sentences (e.g., from “The house is big” to “The house was big”) and observing how the word embeddings changed. In this example, tense change is equivalent to coordinates change in a physical system. For doing the experiment, we have used a set of 39 words and sentences (which we know is a very small dataset, but it’s just for testing purposes). We have tested with 5 words and contexts. We have used cosine similarity and MSE to evaluate the model. To infer the transformation function, we have used a basic linear model and a Multi Layer Perceptron. The results have been the following:

Linear Model Performance:

Neural Network:

For the test, we have used the words 'jump', 'smell’, ‘understand’, ‘believe’ and ‘mountain’, showing the following results:

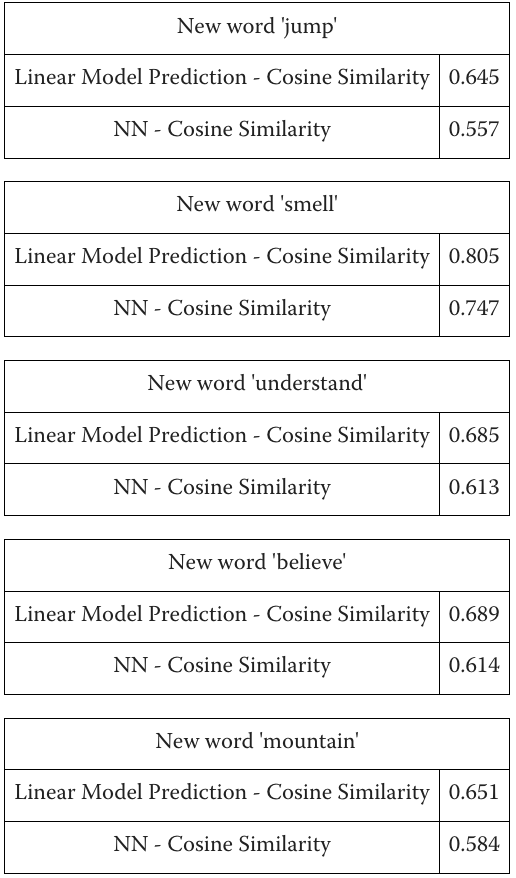
1. These changes could be approximated quite well by simple mathematical transformations.
2. These transformations were consistent across different words and contexts.

This suggests that language models do have some form of “general covariance"—they"understand words consistently across different contexts or coordinates.

Implications for AI Alignment

These findings open up exciting possibilities for AI alignment:

1. By understanding the “symmetries” of a language model, we might predict its behavior more accurately.
2. We could potentially use these symmetries to guide the model towards more desirable outputs.
3. The “conservation laws” of language models might reveal fundamental constraints on their behavior, helping us design safer and more reliable AI systems.

Conclusion

While we’ve only scratched the surface, the analogies between physics and AI are fascinating. Borrowing tools and concepts from physics may provide us with new insights into the complex world of language models. This interdisciplinary approach could be key to developing AI systems that are not just powerful but also consistent with human values and purposes.
Exploring these links opens up a new field in AI research, bridging the gap between natural laws and machine learning structures. The quest to genuinely understand and align AI may take us through the heart of physics itself.

Note 1: You can find a notebook with the experiments here.

Note 2: You can find a more detailed explanation in this paper here.